一阶常微分方程初值问题，一般表示如下所示：

\[\begin{cases} y^{'}=f(x,y)\\ y(x_{0})=y_{0} \end{cases}\]

欧拉法，改进的欧拉法，龙格-库塔法都是基于同样的原理，即用切线\(y^{'}=f(x,y)\)去逼近原方程的曲线\(y=f(x)\)1。

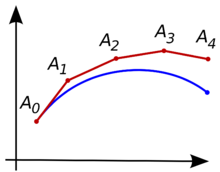
Euler_Method

那么怎么作出切线呢，\(y^{'}=f(x,y)\)就是这个切线的方程。

欧拉法计算时，令每次前进的步长为\(h\)，每次根据步长h根据切线\(f(x,y)\)的方向求下一个\(y\)的位置。

\[\begin{cases} y_{i+1}=y_{i}+hK_{1}\\ K_{1}=f(x_{i},y_{i}) \end{cases}\]

改进的欧拉法，就是在欧拉法的基础上修改方向（斜率），是得每步计算的切线更贴近原曲线。

\[\begin{cases} y_{i+1}=y_{i}+\frac{h}{2}(K_{1}+K_{2})\\ K_{1}=f(x_{i},y_{i})\\ K_{2}=f(x_{i+1},y_{i}+hK_{1}) \end{cases}\]

如果设法在\([x_{i},x_{i+1}]\)内多预报几个点的斜率值，然后将它们加权平均作为平均斜率\(K^{*}\)，则有可能构造出更高精度的计算格式，龙格-库塔法就是在上述改进欧拉法的基础上，继续构造新的\(K\)，来达到更加精确的逼近原曲线的目的。

一般常用的方法是四阶龙格-库塔法，计算公式如下：

\[\begin{cases} K_{1}=f(x,y)\\ K_{2}=f(x_{i+\frac{1}{2}},y_{i}+\frac{h}{2}K_{1})\\ K_{3}=f(x_{i+\frac{1}{2}},y_{i}+\frac{h}{2}K_{2})\\ K_{4}=f(x_{i+1},y_{i}+hK_{3})\\ y_{i+1}=y_{i}+\frac{h}{6}(K_{1}+2K_{2}+2K_{3}+K_{4}) \end{cases}\]

四阶龙格-库塔法程序如下所示。

#include"stdio.h"
#include"stdlib.h"
void fun1(double a,double b,double h)
{  double x,y=0,i,k1,k2,k3,k4;
   for(i=1;i<=((b-a)/h)+1;i++)
 { x=i*h;
   k1=h*(1-y);
   k2=h*(1-(y+1/2.0*k1));
   k3=h*(1-(y+1/2.0*k2));
   k4=h*(1-(y+k3));
   y=y+1/6.0*(k1+2*k2+2*k3+k4);
 }  
 printf("%lf\n",y);
      }
      
void fun2(double a,double b,double h)
{  double x,y=1,i,k1,k2,k3,k4;   
   for(i=0;i<=((b-a)/h);i++)
 { x=i*h;
   k1=h*(x*y*y);
   k2=h*((x+h/2)*(y+1/2.0*k1)*(y+1/2.0*k1));
   k3=h*((x+h/2)*(y+1/2.0*k2)*(y+1/2.0*k2));
   k4=h*((x+h)*(y+k3)*(y+k3));
   y=y+1/6.0*(k1+2*k2+2*k3+k4);
 }  
 printf("%lf\n",y);
      }

int main()
{double a=0,b=1,h=0.1;
      fun1(a,b,h);
      fun2(a,b,h);
      }

  1. 如何理解常微分方程的通解、特解以及所有解？ ↩