这篇也是写代码的一部分，对于 \(\LaTeX\) 的使用，感觉中文排版之前是一个痛点，其他的宏以及类的使用方法看几个例子就足够了。所以这里只记录了如何用 \(Xe\TeX\) 写中文文档。除了中英混排，中日、中韩以及日韩、英日、英韩的混排估计都有类似的排版问题，还需要自己搜索相关资料解决。

\(Xe\TeX\) 支持引擎直接支持 Unicode 字符。别再用什么 CJKutf8 了。 如果你用Linux系统，下载安装\(\TeX Live\) 套装，安装有界面的编辑软件 Gummi，可以完美的撰写中文文档。我觉得使用相关 Windows 环境下的软件，也能完成这个任务。 另外，\(C\TeX\) 宏集做中英文混排据说非常棒，如果无法忍受默认的 \(Xe\TeX\) 排版效果，可以选择 \(C\TeX\) 宏集。对于我来说用最简单的就足够了。

\documentclass{article}
\usepackage{fontspec}
\setmainfont{文泉驿点阵正黑}
\XeTeXlinebreaklocale "zh"
\XeTeXlinebreakskip = 0pt plus 1pt minus 0.1pt
\begin{document}
\title{这是Xe\TeX 编排的中文}
\author{YU Lijia}
\maketitle
Xe\TeX 支持引擎直接支持 Unicode 字符。别再用什么 CJKutf8 了。 如果你用Linux系统，下载安装\TeX Live 套装，安装有界面的编辑软件Gummi，可以完美的撰写中文文档。我觉得使用相关 Windows 环境下的软件，也能完成这个任务。 另外，C\TeX 宏集做中英文混排据说非常棒，如果无法忍受默认的Xe\TeX 排版效果，可以选择C\TeX 宏集。对于我来说用最简单的就足够了。

%\tableofcontents
\section{\TeX Live是什么？}

\begin{tabular}[t]{|l|c|c|}
\hline
对比	& CTeX & TeXLive \\
\hline
操作系统 &	只限于Windows下 &	通用 \\
\hline
制作人 & 中科院吴凌云和其他小伙伴 &	TUG \\
\hline
其他 & 对MiK\TeX 的再封装 & 可刻录在光盘直接运行 \\
\hline
\end{tabular}\\
 
C\TeX 和 \TeX Live都是 \LaTeX 的发行版，包括编译器和配套软件安装包。 C\TeX 已经完全过时。所以发行版一定要选择 \TeX Live。
 
\section{C\TeX 发行版和C\TeX 宏集是什么关系}

C\TeX 发行版是基于MiK\TeX 的 Windows下编译\TeX 文件的软件， C\TeX 宏集是专为中英文混排设计的sty宏包和cls文类的集合。


\end{document}

元旦期间看了两部影片《Soul》和《行骗天下JP：公主篇》，我觉得 Soul 拍得太深奥，不像一部儿童动画电影。影片中反复经历在 The great before、The great beyond、现实的轮回，最有意思的人物是22，她为了寻找自己的Spark（火花），在 The great before 接受了那么多世界公认的专家的指导。相比于男主角来教导22找寻火花，其实最后是22让男主角意识到了火花真正的含义。“鱼与大海”的对话说明我们本来就在海洋里，但仍然认为自己没有找到“海洋”，这段对话对我的启发很大，做好自己的事情，比追寻一个可能不是目标的目标更为重要。

行骗天下这一集的电影，观看的时候带着点悲伤，毕竟里面两位重要配角都在去年去世。整部电影故事一般，但总体上还是欢快带着温馨。据说后面还会拍英雄篇，希望新的剧情给点力。

今年连续更新了4篇水博客。现在我都不敢在开口说什么新的新年计划了，之前的都只完成了一半。自控能力要加强，不要耽误时间。虽然嘴上说着996不好，但是不抓紧时间，吃亏的只能是自己。去年没做完的整理上学期间学习的代码工作在本年内会继续。之前该补的东西，尽量都补上，要不都不好意思开新的坑。

除此之外，还有一条新的经验要牢记：永远不到等到文件夹乱得找不到文件了，再去整理，养成良好的电脑文件归类习惯很重要。先乱放，再整理，是在是太耽误时间了。

人的一生是熵不断增加的过程。整理好自己的用品，安排好各种时间，能降低自己平时生活中的熵（混乱程度）。

再多写一些展望吧。。

• 我最喜欢的 RNA 将在医疗领域发挥更重大的作用（不止是疫苗）。
• 如何让其他星球产生含氧且适宜人类生存的大气层是个研究方向，感觉还没准能成功呢。
• 人机接口这东西，最近还最好先关注一些肢体神经，饶了大脑吧。

互联网公司职工按 996 甚至每月休 2 天的频率来开展工作，因身体和精神原因出事频繁，尤其某个“x多多”近期频繁上新闻。 最近读了马克思的《1844年经济学哲学手稿》，认识到某地还是个“初级”的“资本主义”社会。简直是天天抓理论学习，但永远都是学一套、说一套、做一套。

在《1844年经济学哲学手稿》中马克思提出了异化劳动的观点。异化的最初含义可以理解为“自我外化为非我，从而使原来与自我同一的东西，变成异己的东西”。例如，我创作一件木雕作品，把自己的思想和手艺固化到这个作品里，也就是将自己的“部分思想”和“手艺”同自己分离，形成一件雕塑，变成不是自己的的东西。马克思的观点认为：异化作为社会现象，是与阶级一起产生的，是人的物质生产机器产品变成异己力量，反过来统治人的社会现象。私有制是异化产生的社会根源，社会分工固定是它的自然缘由。在异化活动中，人的能动性丧失了。遭到异己的物质力量或精神力量的奴役，从而使人的个性不能全面发展，只能片面发展，甚至畸形发展。在资本主义社会，异化达到最严重的程度。

资本主义的工厂中，让工人延长上班时间，生产更多的产品，产生更多的利润。但产品的利润归资本家所有，反过来工人只能通过自己劳动所的工资来购买产品。工人为了购买必需品，而进行劳动，这时候，劳动就不是工人“自由自觉”的活动，具有强制性、外在性和异己性。这同互联网行业的996，以及某些实验室的研究生培养，没有任何区别。互联网行业里，大家每天回家就睡个觉，其余时间都在通勤、搬砖、吃喝拉撒，自己的产品获得的利润归资本家所有，而自己只能通过获得的工资来购买产品，期权这些等着解禁还不知要熬过多少年，前提是身体健康情况允许你继续熬。这也是互联网行业35岁以上不要的原因，当不了电池继续发电，自然要淘汰。一些打卡严格的高等教育实验室也是严格规定学生的工作时间，本来收入就只能够吃饭，还可能时常受到精神打击。在这些异化活动里，人的能动性完全丧失了，绝大部分人只能片面的发展。纵观世界，东亚三国，两个资本主义国家、一个社会主义国家，都差不多这样。还真说不好这么“卷”是因为我们自身的发达程度不够，还是人口原因或者文化原因。

马克思根据唯物主义辩证法，唯物史观和剩余价值学说，还论证过资本主义必然灭亡，我不知他看到现今的情况，会不会发表什么新的看法，毕竟他老家的工人待遇比这边的好太多。在发达国家里比较的话，估计 Musk 的公司要排除在外，我觉得他家公司的工作时长应该和我们的 996 有一拼。

一阶常微分方程初值问题，一般表示如下所示：

欧拉法，改进的欧拉法，龙格-库塔法都是基于同样的原理，即用切线\(y^{'}=f(x,y)\)去逼近原方程的曲线\(y=f(x)\)¹。

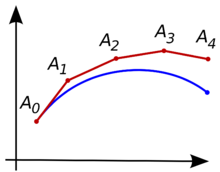
那么怎么作出切线呢，\(y^{'}=f(x,y)\)就是这个切线的方程。

欧拉法计算时，令每次前进的步长为\(h\)，每次根据步长h根据切线\(f(x,y)\)的方向求下一个\(y\)的位置。

改进的欧拉法，就是在欧拉法的基础上修改方向（斜率），是得每步计算的切线更贴近原曲线。

如果设法在\([x_{i},x_{i+1}]\)内多预报几个点的斜率值，然后将它们加权平均作为平均斜率\(K^{*}\)，则有可能构造出更高精度的计算格式，龙格-库塔法就是在上述改进欧拉法的基础上，继续构造新的\(K\)，来达到更加精确的逼近原曲线的目的。

一般常用的方法是四阶龙格-库塔法，计算公式如下：

四阶龙格-库塔法程序如下所示。

#include"stdio.h"
#include"stdlib.h"
void fun1(double a,double b,double h)
{  double x,y=0,i,k1,k2,k3,k4;
   for(i=1;i<=((b-a)/h)+1;i++)
 { x=i*h;
   k1=h*(1-y);
   k2=h*(1-(y+1/2.0*k1));
   k3=h*(1-(y+1/2.0*k2));
   k4=h*(1-(y+k3));
   y=y+1/6.0*(k1+2*k2+2*k3+k4);
 }  
 printf("%lf\n",y);
      }
      
void fun2(double a,double b,double h)
{  double x,y=1,i,k1,k2,k3,k4;   
   for(i=0;i<=((b-a)/h);i++)
 { x=i*h;
   k1=h*(x*y*y);
   k2=h*((x+h/2)*(y+1/2.0*k1)*(y+1/2.0*k1));
   k3=h*((x+h/2)*(y+1/2.0*k2)*(y+1/2.0*k2));
   k4=h*((x+h)*(y+k3)*(y+k3));
   y=y+1/6.0*(k1+2*k2+2*k3+k4);
 }  
 printf("%lf\n",y);
      }

int main()
{double a=0,b=1,h=0.1;
      fun1(a,b,h);
      fun2(a,b,h);
      }